
Group Technology & Research, Position Paper 2018
AI + Safety
Safety implications for Artificial Intelligence
Why we need to combine causal- and data-driven models
WHEN TRUST MATTERS
Contributors
Christian Agrell, MSc., Andreas Hafver, PhD., Frank Børre Pedersen, PhD.
(DNV, Group Technology & Research)
Image credits
Image credits are linked at individual images where applicable
Published
2018-08-28
Copyright© 2018 DNV ®, DNV terms of use apply.
Executive summary
No one really knows how the most advanced algorithms do what they do. That could be a serious problem as computers become more responsible for making important decisions.
Will Knight
"The Dark Secret at the Heart of AI" - MIT Technology Review, April
11, 2017
Artificial Intelligence (AI) and data-driven decisions based on machine-learning (ML) algorithms are making an impact in an increasing number of industries. As these autonomous and self-learning systems become more and more responsible for making decisions that may ultimately affect the safety of personnel, assets, or the environment, the need to ensure safe use of AI in systems has become a top priority.
Safety can be defined as "freedom from risk which is not tolerable" (ISO). This definition implies that a safe system is one in which scenarios with non-tolerable consequences have a sufficiently low probability, or frequency, of occurring. AI and ML algorithms need relevant observations to be able to predict the outcome of future scenarios accurately, and thus, data-driven models alone may not be sufficient to ensure safety as usually we do not have exhaustive and fully relevant data.
DNV acknowledges that sensor data and data-driven models will become integral to many safety-critical or high-risk engineering systems in the near future. However, as pointed out in W. Knight, 2017, it is inevitable that failures, and, consequently, accidents, will still occur. However, the data-driven era is unique with respect to our capability of learning from failures — and of distributing that learning further. As an industry, we do not want to learn only from observation of failures. DNV has extensive experience in utilizing our causal and physics-based knowledge to extract learning from severe accident scenarios, but without those accidents actually occuring. This position paper discusses aspects of data-driven models, models based on physics and logic, and the combination of the two.
1) We need to utilize data for empirical robustness. High-consequence and low-probability scenarios are not well captured by data-driven models alone, as such data are normally scarce. However, the empirical knowledge that we might gain from all the data we collect is substantial. If we can establish which parts of the data-generating process (DGP) are stochastic in nature, and which are deterministic (e.g., governed by known first principles), then stochastic elements can be utilized for other relevant scenarios to increase robustness with respect to empirically observed variations.
2) We need to utilize causal and physics-based knowledge for extrapolation robustness. If the deterministic part of a DGP is well known, or some physical constraints can be applied, this can be utilized to extrapolate well beyond the limits of existing observational data with more confidence. For high-consequence scenarios, where no, or little, data exist, we may be able to create the necessary data based on our knowledge of causality and physics.
3) We need to combine data-driven and causal models to enable real-time decisions. For a high-consequence system, a model used to inform risk-based decisions needs to predict potentially catastrophic scenarios prior to these scenarios actually unfolding. However, results from a complex computer simulations or empirical experiments are not usually possible to obtain in real-time. Most of these complex models have a significant number of inputs, and, because of the curse-of-dimensionality, it is not feasible to calculate/simulate all potential situations that a real system might experience prior to its operation. Thus, to enable the use of these complex models in a real-time setting, it may be necessary to use surrogate models (fast approximations of the full model). ML is a useful tool for creating these fast-running surrogate models, based on a finite number of realizations of a complex simulator or empirical tests.
4) A risk measure should be included when developing data-driven models. For high-risk systems, it is essential that the objective function utilized in the optimization process incorporates a risk measure. This should penalize erroneous predictions, where the consequence of an erroneous prediction is serious, such that the analyst (either human or AI) understands that operation within this region is associated with considerable risk. This risk measure can also be utilized for adaptive exploration of the response of a safety-critical system (i.e., as part of the design-of-experiments).
5) Uncertainty should be assessed with rigour. As uncertainty is essential for assessing risk, methods that include rigorous treatment of uncertainty are preferred (e.g., Bayesian methods and probabilistic inference).
DNV is convinced that the combination of data-driven models and the causal knowledge of industry experts is essential when AI and ML are utilized to inform, or make, decisions in safety-critical systems.
AI safety - current status
From May 2018, the EU General Data Protection Regulation (GDPR) became enforceable, and applies to all companies and organizations that "offer goods or services to, or monitor the behaviour of, EU data subjects." Many consider GDPR to be the first major international legal step by which AI is held accountable and must provide an explanation for decisions (see, e.g., T. Revell, 2018).
The metric of efficacy of AI and ML algorithms has previously been based on predicative power alone. However, we now require that they also adhere to human ethical principles and that erroneous predictions do not lead to unintended negative consequences. Google Brain researchers have published a good discussion on:
Concrete Problems in AI Safety (click to expand)
- Avoiding negative side effects:
- How to ensure that the AI agent does not affect its environment in a negative way while pursuing its goals.
- Avoiding reward hacking:
- How to ensure that the AI agent does not game its reward function.
- Scalable oversight:
- How the AI agent can efficiently respect aspects of the objective that are too expensive to be frequently evaluated during training.
- Safe exploration:
- How the AI agent can explore different strategies and scenarios while ensuring that these strategies or scenarios are not detrimental to its environment.
- Robustness to distributional shift:
- How to ensure that the AI agent recognizes and behaves robustly when exposed to a scenario that differs from that of its training scenarios.
D. Amodei et al., 2016 (paraphrased)
Concrete Problems in AI Safety
Microsoft discusses a set of ethical principles that should act as a foundation for development of AI-powered solutions to ensure that humans are put at the centre in:
The Future Computed: Artificial Intelligence and its role in society
- Fairness:
- To ensure fairness, we must understand how bias can affect AI systems.
- Reliability:
- AI systems must be designed to operate within clear parameters and undergo rigorous testing to ensure that they respond safely to unanticipated situations and do not evolve in ways that are inconsistent with the original expectations.
- Privacy and security:
- AI systems must comply with privacy laws that regulate data collection, use, and storage, and ensure that personal information is used in accordance with privacy standards and protected from theft.
- Inclusiveness:
- AI solutions must address a broad range of human needs and experiences through inclusive design practices that anticipate potential barriers in products or environments that can unintentionally exclude people.
- Transparency:
- Contextual information about how AI systems operate should be provided such that people understand how decisions are made and can more easily identify potential biases, errors and unintended outcomes.
- Accountability:
- People who design and deploy AI systems must be accountable for how their systems operate. Accountability norms for AI should draw on the experience and practices of other areas, such as healthcare and privacy, and be observed both during system design and in an ongoing manner as systems operate in the world.
Microsoft (paraphrased)
The Future Computed: Artificial Intelligence and its role in society - Executive Summary
The US Defence Advanced Research Projects Agency (DARPA) highlights that AI needs to be explainable to humans in order to create the appropriate level of trust, and runs a special project on this: the XAI project - Explainable Artificial Intelligence.
However, one aspect of ML and AI that is often not given appropriate attention is beautifully expressed by Cathy O'Neil:
Big Data processes codify the past. They do not invent the future.
Cathy O'Neil
"Weapons of Math Destruction: How Big Data Increases Inequality
and Threatens Democracy", 2017
In her aptly named book "Weapons of Math Destruction", she exemplifies many of the aspects discussed by Google Brain and Microsoft. She explains how algorithms - which, in theory, should be blind to prejudice, judge according to objective rules, and eliminate biases - actually might do the opposite.
Since these algorithmic models are based on historical data, they not only incorporate previous discriminations and biases - they reinforce them. She explains how these algorithmic "Weapons of math destruction" are used to grant (or deny) loans, to set parole dates or sentence durations, and to evaluate workers, teachers, or students, and how vicious feedback loops are created. Students from poor neighbourhoods may, for example, be denied loans that could have helped them obtain an education that could, in turn, have brought them out of poverty.
One of the problems is that many of these models confuse correlation with causation, and to base decisions on correlations alone is one of the major pitfalls in the analysis of data (see, e.g., J. Pearl, 2010a).
Since many of the ML and AI models used today are opaque, incontestable, unaccountable, and unregulated, Cathy O'Neil calls on modelers to take more responsibility for their algorithms.
This is a position that DNV supports, and although the GDPR is aimed at protecting natural person(s), it is prudent to apply the same principles to engineering systems.
As illustrated above, the field of AI safety is broad, and an active area of research. This position paper complements the discussion by focusing on complicating factors and possible solutions when AI and ML are utilized within a safety context (i.e., to inform or make decisions in safety-critical systems - for example controlling industrial assets). Rather than considering the general safety of AI, here we discuss the implications of using AI and ML in low-probability and high-consequence scenarios.
How we (and AI) learn
All models are wrong, but some are useful.
George Edward Pelham Box
"Robustness in the strategy of scientific model building",
1979
In their 1987 book Computer Simulation of Liquids, Allen and Tildesley illustrated the connection between experiments (and experience), theory and computer simulations, for how to gain and improve knowledge of a real system. Similar connections between real-world observations and data-driven models are equally relevant, and Figure 5 illustrates these connections (based on the original figure by Allen and Tildesley).

Figure 1: The connection between experiments (and experience), theory, computer simulations, and data-driven models.
They argued that the more difficult and interesting the problem, the more desirable it becomes to have as close to an exact solution to the problem as possible. For complex problems, this may only be tractable through computer simulations, and, as the computational power and finesse in modelling have increased, the engineering community has been able to develop extremely accurate and strongly predictive simulation models. The engineers recognized computer experiments (simulations) as a way of connecting the microscopic details of a system to the macroscopic properties of experimental interest.
Similarly, the revolution of Big Data analytics has shown the efficacy of data-driven models when predicting individual outcomes based on large collections of observed data. This is also a good example of a bridge between individual (microscopic) entities and the real-world macroscopic observations.
Learning occurs for both us, humans, and AI or ML algorithms, on the basis of a cycle where we observe real-world data, construct a model, use the model to predict a real-world outcome, and finally improve our models by comparing the predictions with actual observations. This learning process should be done in accordance with the principles of the scientific method: allowing the models to be falsifiable, and continuously testing and improving them. In this way the current collection of knowledge is advanced.
However, the aphorism of George Box that all models are wrong, but some are useful is still important when assessing the confidence in the results from our models.
Data is good, but not enough
Big data analytics has shown both its worth and its potential for a negative impact in several application areas over the last decade. Some of the best known applications are targeted marketing - as illustrated in the NY Times article "How Companies Learn Your Secrets" or the recent Facebook - Cambridge Analytica scandal related to the 2016 US presidential campaign (first reported by The Guardian, 11. Dec. 2015, and more recently by NY Times, 8. Apr. 2018). Other uses are, for example, recommendation engines used by companies like Netflix and Amazon to suggest similar or related goods or services, and, of course, the algorithms that make your Google searches so "accurate" that you seldom need to go beyond page one of your search results!
The engine behind this data-driven revolution is machine learning (ML). ML is by no means a new concept - the term was coined by A.L. Samuel, 1959 - and can loosely be thought of as the class of algorithms that build models based on a statistical relationship between data; (see P. Domingos, 2012 for an informal introduction to ML methods and the statistical background, or T. Hastie et al., 2009 for a more comprehensive treatise). The goal of an ML model in a data-analytics setting is to provide accurate and reliable predictions, and its most prominent and wide-spread use is focused on consumer markets - where data are Big.
The capitalizations in these consumer markets, by the revolutionary use of ML and data analytics, are usually hallmarked by small gains that accumulate across an entire population of consumers.
The best minds of my generation are thinking about how to make people click ads. That sucks.
Jeff Hammerbacher, interviewed by Ashlee Vance
"This Tech Bubble is Different" - Bloomberg Businessweek, April
14, 2011
For high-risk systems, characterized by high-consequence and low-probability scenarios, the situation is quite different. The potentially negative impact may be huge, and erroneous predictions might lead to catastrophic consequences.
Standards of empirical evaluation
Data-driven decisions are based on three principles in data science: predictability, computability, and stability (B. Yu, 2017). In addition, and particularly important for safety-critical systems, the consequences of erroneous predictions need to be assessed in a decision context.
Prediction is a requisite if an AI or ML algorithm is going to be used in a decision context. Together with cross validation (CV), it makes a human-interpretable validation of the applied model for a certain application. In order to have good prediction accuracy, it is important that the model is developed based on sufficient relevant data from the data-generating process (DGP), (i.e., the process that generates the data that one wants to predict). It is also important that the DGP is computationally feasible, i.e., that an algorithm exists that can learn the DGP from a finite set of training data (see, e.g., A. Blum and R.L. Rivest, 1988).
If the above requisites are met, and an erroneous prediction has a sufficiently negative consequence to be unwanted, the last principle is stability. This is the major problem with safety-critical decisions based on data-driven models. For valid predictions, the future scenarios need to be stable with respect to the data from which the prediction model was trained. At the same time, data related to high-consequence scenarios are, thankfully, scarce. In line with Cathy O'Neil's argument above, this makes ordinary data-driven methods inappropriate for decision making in the context of unwanted and rare scenarios.
In a recent position paper by Google AI researchers, D. Sculley et al., 2018, it is argued that "the rate of empirical advancement may not have been matched by consistent increase in the level of empirical rigor across the [ML] field". They point to the fact that "empirical studies have become challenges to be “won” [e.g. as competitions on Kaggle], rather a process for developing insight and understanding". In addition to current practices, they suggest a set of standards for empirical evaluations that should be applied when using ML:
- Tuning Methodology:
- Tuning of all key hyperparameters should be performed for all models including baselines via grid search or guided optimization, and results shared as part of publication.
- Sliced Analysis:
- Performance measures such as accuracy or AUC [Area under curve of Receiver operating characteristic (ROC)] on a full test set may mask important effects, such as quality improving in one area but degrading in another. Breaking down performance measures by different dimensions or categories of the data is a critical piece of full empirical analysis.
- Ablation Studies:
- Full ablation studies of all changes from prior baselines should be included, testing each component change in isolation and a select number in combination.
- Sanity Checks and Counterfactuals:
- Understanding of model behavior should be informed by intentional sanity checks, such as analysis on counter-factual or counter-usual data outside of the test distribution. How well does a model perform on images with different backgrounds, or on data from users with different demographic distributions?
- At Least One Negative Result:
- Because the No Free Lunch Theorem still applies, we believe that it is important for researchers to find and report areas where a new method does not perform better than previous baselines. Papers that only show wins are potentially suspect and may be rejected for that reason alone.
D. Sculley et al., 2018
Winner's curse? On pace, progress, and empirical rigor
These standards are crucial when applying ML and AI in safety-critical systems to ensure that the models are trained on sufficient and relevant data to be able to generalize their predictions to rare and potentially catastrophic scenarios.
In addition to these standards, DNV argues that ML and AI model predictions should also adhere to established scientific (physical or causal) knowledge about the system (or DGP) as outlined in section Guide the AI - impose constraints.
High-risk scenarios and lack of data
The nature of - and our engineering approaches to cope with - systems that can exhibit high-risk scenarios, ensure that we lack, or have very little, relevant data. To be able to investigate these high-risk scenarios prior to their occurrence (i.e. when we lack data), an artificial agent needs to be able to answer counterfactual questions, necessitating retrospective reasoning (see, e.g., J. Pearl, 2018a).
To illustrate how lack of data limits the usefulness of data-driven models, we will use the game of golf as a well-known example of a data-generating process.
In this paper, Pearl highlights the extremely useful insight unveiled by the logic of causal reasoning, that causal information can be classified into three sharp hierarchical categories based on the kind of questions that each class is capable of answering (J. Pearl, 2018a):
-
1. Association:
-
Prediction based on observations, characterized by conditional probability sentences like, e.g., the probability of event Y=y given that we observe event X=x.
This typically answers questions like "What is?". This is based purely on statistical relationships, defined by the naked data (observations), and is where many ML systems operate today.
Example: What is the expected off-the-tee driving distance of a golf ball on the PGA Tour given the observations of previous PGA Tour(s)?
Association cannot be utilized without existing and relevant data.
-
2. Intervention:
-
Prediction based on intervention, characterized by, e.g., the probability of event Y=y, given that we intervene and set the value of X to x and subsequently observe event Z=z.
This typically answers questions like "What if?". This class does not only see what is, but also includes some kind of intervention.
Example: What would be the expected off-the-tee distance of a golf ball if we intervene and require all players to use a 5-Iron club at tee-off?
Such questions also cannot be answered without existing and relevant data. We need, at the least, to obtain data on 5-Iron club shots, if not 5-Iron club shots from the tee.
-
3. Counterfactuals:
-
Prediction based on imagination and retrospect considerations. This is characterized by e.g. the probability that event Y=y had been observed had X been x, given that we actually observe X to be x' and Y to be y'.
This typically answers questions like "Why?" or "What if we had acted differently?". This class necessitates retrospective reasoning or imagining.
Example: How far would a drive shot travel on the moon?
As we only have observed the drive distances here on Earth, questions of this sort can only be answered if we possess causal knowledge of the process. This can be either through functional or structural equation models or their properties (J. Pearl, 2010b).
This hierarchy of causal information has strong parallels to the Data-Information-Knowledge-Wisdom (DIKW) pyramid.
Where is the wisdom we have lost in knowledge?
Where is the
knowledge we have lost in information?
T.S. Elliot
"The Rock", 1934
The DIKW pyramid implies that knowledge and wisdom are extracted from the lower levels of data and information, although the truth may be much messier - including social, goal-driven, contextual, etc. processes, and by being wrong more often than right (see, e.g., D. Weinberger, 1010). The bottom line is:
Data might lead to knowledge - but with causal knowledge, data can become more easily available!
EXAMPLE: Golf on the moon
Golf is a sport where the flight dynamics of the golf ball are an important aspect of the game. It has thus been scrutinized through countless studies over the years. The flight of a golf ball is essentially governed by a fairly simple ordinary differential equation (ODE):

where 



Some of these variables are purely stochastic, in the sense that it is impossible to know before the hit which value it will assume - like the off-centre aim. Some variables are close to being purely deterministic, i.e., known with a high degree of certainty - like the mass of the golf ball and the gravitational constant. Other variables are a combination; for example, the spin of the ball and the launch angle are clearly dependent on the selected club, but there is a stochastic element to the variation that can not be determined prior to the hit.
The result of one realization of these variables will end up as one point of distance travelled in the x- and y-direction. For a normal PGA tournament, with 156 players playing 18 holes, this amounts to 8500 shots with various clubs (with an average of 3 strokes per hole, not including the putt).
Figure 2 in the Golf-shot data tab below plots the distance of each of the 8500 shots, while Figure 3 in the Physical model tab also includes example trajectories for each club calculated with the ODE model mentioned above.
A golfer needs to decide which club she should use for her next shot. Her caddy will suggest a club based on several factors, where one of the most important is the remaining distance to the green. This is a typical decision process at which a data-driven model trained on shot data excels. However, if the next tournament were to be played on the moon, the data-driven caddy would be at a loss - no relevant data exist (except one shot by Alan Shepard in 1971).
However, by introducing causal knowledge about the problem at hand, we can assist the data-driven model. Figure 4 in the Golf on the moon tab shows the ranges of different clubs, adjusted for similar swing velocities, on Earth (dots) and on the moon (lines). On Earth, the longest drive distance is obtained with a club that has a low launch angle and low backspin on the golf ball. A high back spin induces lift which will slow the ball in the x-direction. Backspin is mainly induced by the loft angle of the club, and a higher loft angle will generally lead to a higher spin on the golf ball. However, on the moon, the atmosphere is extremely thin, and the spin will not affect the trajectory of the golf ball. Thus, on the moon, the club with the loft angle that gives the highest launch angle (up to 45°) will travel farthest - contrary to what we experience on Earth.
Figure 2: Distance x and off-axis distance y of all shots (excluding putting) in a synthetic PGA tournament.
Figure 3: Distance x and off-axis distance y of all shots (excluding putting) in a synthetic PGA tournament, with examples of trajectories calculated based on known physical behaviour.
Figure 4: Distance x of typical tee-off shots with simulated trajectories calculated based on known physical behaviour on the Earth (dots) and on the moon (lines). Notice how the PW is the shortest shot on Earth and the longest on the moon.
Robust empiricism and extrapolation
The golf-on-the-moon example above illustrates two different and important aspects of data-driven and physics-based models.
Data-driven models are needed to extract the effect of variations across a large population for multiple inputs. The stochastic elements, both from the input side and the data-generating process itself, can be utilized for other relevant scenarios to increase the robustness with respect to empirically observed variations.
Physics-based models do not provide any information on the variation across its inputs. However, given a set of inputs, they can be reliably used to extrapolate outside the domain where no previous data exist. This increases the robustness and confidence associated with extrapolation.
To be able to ensure safe operations for systems that might enter high-consequence scenarios with low probability we need to create data where no data exist, just as we did for the golf hit on the moon. This can only be done safely by careful considerations of our causal knowledge and cautious exploration of the unknown.
For complex systems, we need to distinguish between aspects that we can explain by causal models and those that are so complex or chaotic that knowledge is most easily extracted by analysing data. We need to combine the best of our causal knowledge with the increasing opportunities that are provided by data analytics.
DNV works to bridge our expert causal models with new data-driven models, which will be paramount for understanding and avoiding the high-risk scenarios that we have pledged to safeguard against. Our aim is to make sure that systems that are influenced by AI are SAFE!
Real-time decisions, uncertainty, and risk
Many of the engineering systems that have been developed, and will be developed, may result in serious consequences if they fail (e.g., do not operate as intended). These systems range from a single individual relying on the anti-lock braking system and traction control of a car, through hundreds of people blissfully unaware of the collision-avoidance systems at work in commercial airplanes, to emergency shut-down systems of nuclear power plants.
Historically, the safety of such systems has been addressed by careful scrutiny of potential scenarios to which the system can be subjected, and cautious engineering of the capacity of these systems. And, although many processes have been automated, it is people who oversee the entire system and thus hold the ultimate responsibility. But this is no longer the case.
As the complexity of our engineering systems increases, and more and more of our systems are interconnected and controlled by computers, our human minds have become hard pressed to cope with, and understand, this enormous and dynamic complexity. In fact, it seems likely that we will be unable to apply human oversight to many of these systems at the timescale required to ensure safe operation. Thus:
Machines need to make safety-critical decisions in real-time, and we, the industry, have the ultimate responsibility for designing artificially intelligent systems that are safe!
Assurance of high-risk and safety-critical systems that rely on ML methods is receiving greater attention (see current status and, e.g., A. Brandsæter and K.E. Knutsen, 2018). C. Agrell et al., 2018 highlights three critical challenges when applying ML methods to high-risk and low-probability scenarios:
-
A high-risk scenario reduces the tolerance for erroneous
predictions.
We cannot accept a decision, that may have catastrophic consequences being based on faulty predictions of an ML algorithm or AI agent. -
Critical consequences are often related to tail events - for
which data are naturally scarce.
ML methods require data. If the data are scarce, the uncertainty associsated with the predictions will be high, and the predictive accuracy significantly reduced. -
ML models that are able to fit complex data well are often
opaque and impenetrable for human understanding.
This makes the model inscrutable and less falsifiable. For a decision maker in a high-risk context, this increases the uncertainty and thus reduces her ability to trust the model.
The first two points are in direct contrast to the typical ML applications that are in use today (e.g., non-consequential recommendation engines etc.). The last point, on lack of transparency in the ML models, relates to how easy it is to quantify the model discrepancy and the ability to falsify models that do not comply with observations. Together, these will affect the approach to validation and quality assurance of high-risk and safety-critical systems under ML or AI influence.
DNV argues the paramount importance of combining causal and data-driven models to ensure safe AI decisions. Just as the physics-based and causal models increase the confidence and accuracy of ML models, it is equally important that we manage to utilize data-driven methods to increase the robustness with respect to stochastic variations. The following discussion is thus limited to the class of problems to which we have access, at least in principle, to causal knowledge - how the physics work, and the associated consequences.
However, two aspects of physics-based models make them ill suited for practical use in a real-time, risk-based decision context:
-
For a high-consequence system, a model used to inform risk-based decisions needs to predict potentially catastrophic scenarios prior to the scenario actually unfolding. The run-time of these complex models is usually significant, sometimes several days, and thus it is not possible to initiate the required analysis in real-time.
-
When a model cannot be run in real-time, an alternative may be to run it in advance. However, as most of these complex models have a significant number of inputs, the curse-of-dimensionality means that it is not feasible to calculate/simulate all the potential situations that a real system might experience prior to its operation.
These challenges are at the heart of making sure that systems influenced by AI are safe.
SpaceX learning cycle

On Tuesday February 6th 2018, SpaceX successfully launched the world's biggest rocket, Falcon Heavy, and landed the two first-stage side boosters safely back on the launch pad in the upright position - ready for refurbishing and new flights.
No full-system test was possible prior to the launch. The team of engineers relied on computer models, together with previous experience of similar systems and advanced ML models, to simulate how the launch would play out and to determine how to control the actual boosters back to the launch pad. This is a perfect example of what can be achieved through extensive use of models based on both causal knowledge and data-driven methods, making autonomous real-time adjustments (see L. Blackmore, 2016 for details on the precision landing of Falcon 9 first stages).
Note, however, that safe landing of the first stages was not achieved on the very first attempt. The video below illustrates well how SpaceX utilized the continuous learning cycle presented in Figure 1 to achieve their ambitious goals.
The Falcon Heavy core booster was supposed to land upright on a drone ship in the Atlantic, but missed by 90 meters and crashed into the ocean (watch on YouTube).
This illustrates two important aspects. First, even when we have designed and tested something thoroughly and in extreme detail, there is always an element of stochastic variation that is difficult to foresee. Six days after the launch Musk tweeted "Not enough ignition fluid to light the outer two engines after several three engine relights. Fix is pretty obvious." There are many possible reasons as to why the core booster had too little ignition fluid. It could be on the provisioning side - not filling the fuel tanks sufficiently before launch; or it could be related to environmental loads - maybe winds caused the controls to use more fuel than anticipated; or it could be any other of a multitude of reasons. This underpins that:
It is "easy" to make something work, but it can be near impossible to ensure that it will not fail!
When we arrive at this acknowledgment, the second aspect follows logically. When our system might fail, we need to understand and address the associated risk. That is why the Falcon Heavy was launched (east bound to utilize Earth's rotation) out of cape Canaveral Air Force Station (map) on the east cost of Florida. This ensured that any failures resulting in a crash of the massive rockets would mean that only oceans would be hit.
It is obvious that hazardous systems must be designed with safety and risk in mind - which we have done for decades, if not centuries. However:
As we move towards more autonomous systems with AI agents making safety-critical decisions, it is paramount that the data-driven models also treat uncertainties with rigour and incorporate risk measures in the decision making process.
Explore and learn a system
The first step of developing safe systems is to establish safe and unsafe system states, and assess how the possible operational states overlap with these.
Most systems are designed to perform a certain spectrum of tasks within a set of specified operational limits. For single-task systems with few operational variables, exploration of the system response is reasonably straight-forward. However, for complex systems performing multiple tasks in a high-dimension input space, such exploration becomes increasingly difficult. With a limited amount of testing effort available, we need to direct our resources wisely to ensure that the overlap between all potential operational scenarios and all possible scenarios leading to failure are sufficiently small.
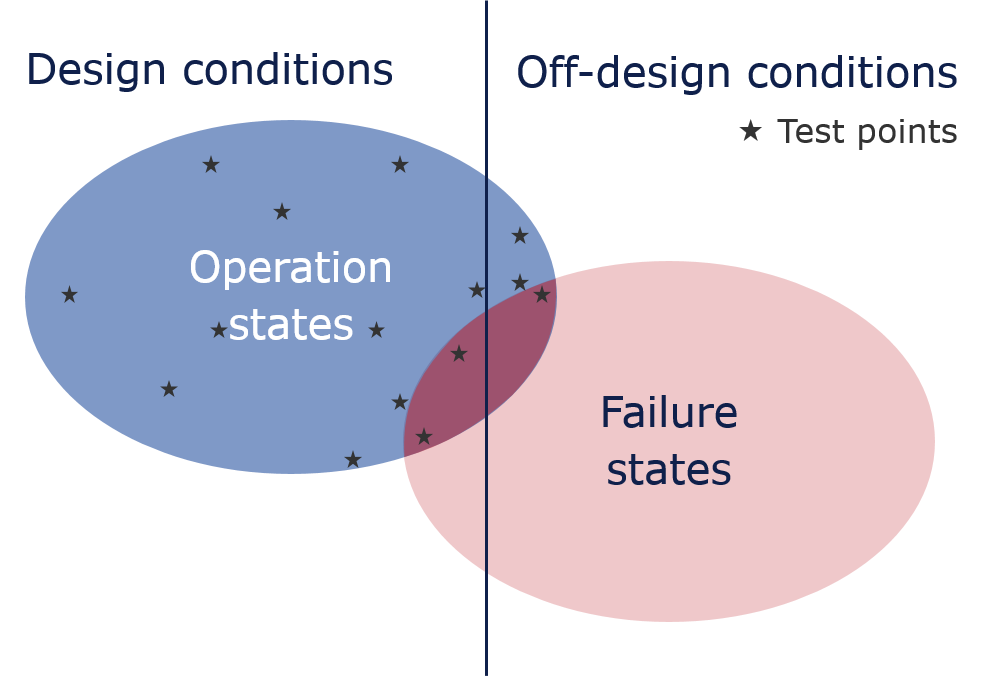
Figure 6: The blue ellipse represents all possible scenarios that the system can enter during its operational life, and the red ellipse indicate all possible scenarios that would lead to a failure of the system. Test points are indicative.
Figure 6 - detailed description
Figure 6 shows a Venn diagram of three overlapping sets and their complement sets. The left half of the figure is the set of scenarios that lies within the design conditions (or the design envelope). This includes all possible scenarios that are within the design limits stated by the designer of the system. The right half of the figure includes all those scenarios that are outside these design limits, i.e., the complement of the design conditions. The blue ellipse represents all possible scenarios that the system can enter during its operational life. This also includes unforeseen scenarios, or scenarios that have been assessed to have a low probability of occurring, and thus the blue ellipse is not entirely contained by the design conditions. Similarly, the red ellipse represents all possible scenarios that will lead to a failure of the system. A good design process seeks to minimize the overlap between the operational regions and the failure regions.
From a risk perspective, the dark-red overlap of the operational and failure regions can only be accepted if the probability of entering these scenarios is sufficiently low, or the associated consequence is acceptable. Assessing the risk of these scenarios is usually considered through quantitative risk analysis (QRA) or structural reliability analysis (SRA) methods (O. Ditlevsen, H.O. Madsen, 1996). However, this region might also contain scenarios that have not been identified and subsequently assessed - posing an unknown risk to the system.
The probability of entering operational states in this region and the associated consequences determine how critical this is with respect to the risk exposure.
As indicated above, the blue region does not pose a threat. As the system is consecutively explored, attention to these regions can, from a safety (or risk) perspective, be reduced. The dark-red region is within what the system might experience through its lifetime, and the aim of the design process is to expose and assess the consequences of entering this region and its associated uncertainty. For increasingly complex systems this might, however, become very difficult. Exploration around this region should usually focus on establishing where the failure limit lies, and assessing the likelihood of a transition from a safe state in the blue region into an unsafe state in the dark-red region.
As the moose-test example below shows, some systems might be designed in such a way that a specific combination of values for different input variables may lead to unintended and possibly dangerous scenarios. As the complexity of a system increases, the chances of not identifying a combination of input variables that leads to an unfortunate and possibly dangerous scenario increase. These are dangerous, unknown scenarios that any design process should aim to expose, and will be further discussed in the section on Design of experiments.
The aim of the design process is to ensure that the risk associated with entering the overlapping region between the operational scenarios and the failure scenarios is sufficiently small to be considered acceptable with respect to the gain represented by the operation of the system.
The stars indicate points in the operational space where the system has been evaluated to learn and explore its response. An efficient exploration, from a safety perspective, is hallmarked by spending some effort to explore the whole operational space, but focusing on establishing the failure limit. In Figure 6, this can be seen as a sparse exploration far away from the failure regions (3 and 4), whereas more tests have been conducted close to-, on-, or just inside the failure regions. As a system is put into operation, the operator can gain more information on the system response and continue learning.
EXAMPLE: The moose test
In 1997, Mercedes-Benz introduced the A-class in the compact car segment. This model became infamous after the Swedish magazine "Teknikens Värld" discovered that the car flipped during an evasive manoeuvre (known as the "moose test") at relatively low speeds. Although Mercedes-Benz first tried to diminish the problem, they later admitted that the A-class had a problem, recalled already sold cars, suspended sales for three months and redesigned the chassis and suspension, and added an advanced electronic stabilization system usually only found in high-end Mercedes-Benz cars (E.L. Andrews, 1997, The Economist, 1997). The Economist reported that the delay would cost approximately DM300m (US$ 175m), which was an additional cost of 12% of the original development cost of DM 2.5 billion.
As can be seen in the video below, 19 years later, other manufacturers are still struggling with this issue
How could such a failure have been overlooked by the developing engineers?
The physics of a tipping car during an evasive manoeuvre is, in its simplest form, a consideration of conservation of moments and forces. During a turn the car is subjected to forces due to its inertia and frictional forces between the road and the tyres. For a mass, m (the car), moving at tangential speed, v, along a path with radius of curvature, r, the centripetal force, which is balanced by the "fictitious" centrifugal (or inertia) force, is described by:

The same mass m will also experience the gravitational force, mg, where g is the gravitational acceleration experienced on the surface of the Earth. The gravitational force is balanced by the normal force, N, between the wheels and the ground surface. The maximum frictional force between the vehicle and the surface is expressed by:

where 
As soon as the centrifugal force becomes larger than the friction force, the vehicle will start to slide outwards in the turn. Similarly, both the centrifugal force and the gravitational force create torques around each of the wheels. To avoid tipping, these torques need to balance. Just before the vehicle overturns, all torques and forces are carried by one set of wheels (i.e. the outer wheels). In this situation, the inertial and gravitational torque is,

respectively, where h is the height of centre of mass (CM) and b is the half width of the wheel base (see Figure 7).
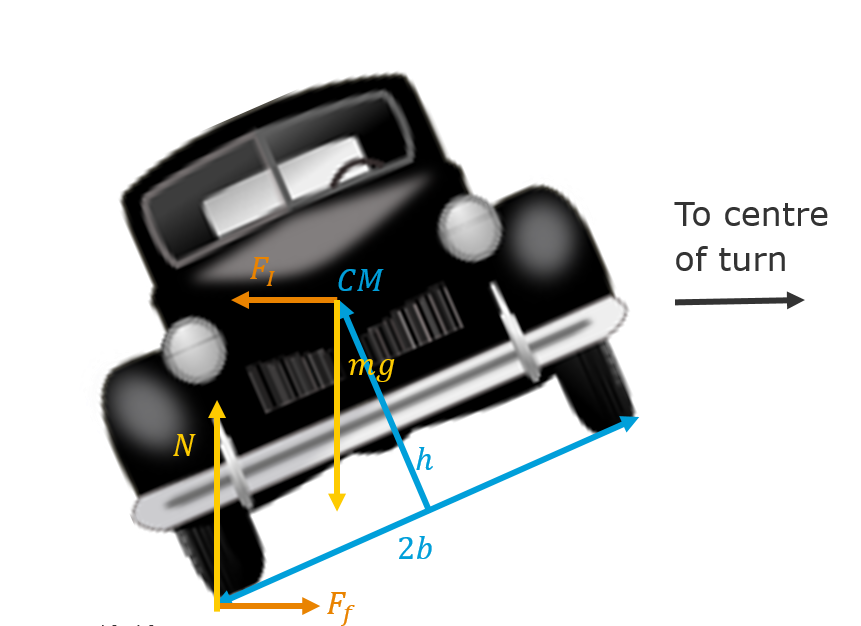
Figure 7: Forces acting on a car in a constant turn at constant speed.
Based on this, it is possible to express the maximum speed a car can have without tipping or skidding as:

It is acknowledged that the physics of a car is more complex than the rigid body consideration used here. However, the physics is well known and it should be fairly simple to check the lowest speed at which a car could tip when performing an evasive manoeuvre within the operational limits of the car - prior to building the actual car and testing it live.
This example illustrates the need for objective methods that systematically explore the outskirts of plausible combinations of operational variables. If a method explores all possible operational scenarios a designer can assess whether a subset of these are implausible, and thus not needed to be handled by design (i.e., most customers would accept that a car driving at its maximum speed cannot also make a minimum radius turn, but they would not accept that it could overturn at the moderate speeds shown in the moose test). This way of excluding scenarios is a more reliable approach than trying to identify critical scenarios prior to exploring the system response, and will eliminate softer factors related to individual designer expertise, experience, and vigilance.
Two objectives are of interest when exploring and learning the behaviour of a system. The first objective is related to optimization of the system's operation - that is, to learn where the system operates most effectively to achieve its primary goal. The second objective is to ensure that the system has a sufficient level of safety. For safety-critical and high-risk systems, the second objective takes precedence.
Learning the possible, and critical, operational states of a system (from data, physics-based models, and controlled experiments) is crucial for a system that will rely on real-time AI decisions. As discussed above, expensive and time-consuming simulations (or experiments) are ill suited to informing the AI in real-time, and this should mainly be completed prior to setting the AI-influenced system in operation. (Note, however, that the AI can be re-trained as new data become available. However, if the new data are from a critical situation, it might be too late for that instance of the system).
The following section outlines a methodology and tool set to guide a more complete and objective exploration of the operational state-space of a system, while optimizing the testing and simulation efforts.
To enable real-time decisions for safety-critical systems, DNV argues that the industry must combine its extensive causal knowledge with more data-driven approaches, and, at the same time, address both uncertainty and risk. DNV suggests the following steps to facilitate the assurance of AI-influenced systems.
Adaptive virtual system testing - ADVISE
To ensure that a system does not fail, it is essential to understand the critical capabilities of the system and the range of scenarios to which the system might be subjected during its operation. For example, an offshore wind turbine needs to have the structural strength (capability) to withstand a range of weather and sea-states (scenarios); It must also be controllable (logic capability) to adapt to changing wind directions and wind speeds, or power demands. It must also be resilient to scenarios that are not part of the normal operational mode, like ship collisions or extreme storms.
For systems for which extensive operational (and failure) data exists, and the current application is going to be operated sufficiently within the limits of the existing data (or the consequences are sufficiently trivial), this might be enough to inform decisions. However, in order to be able to operate a high-risk system with confidence, we need to explore and understand as much as possible the potentially hazardous scenarios that the system may enter. As this knowledge might be too expensive or dangerous to obtain through real-world data, we have to rely on our causal and physics-based (virtual) models to gain the necessary insights.
In a high-risk decision context, two very real limitations affect how we need to relate to simulation or test results. The first, and most obvious, is to be able to describe the extent of accuracy of the model - i.e., to understand the associated model uncertainty. The second limitation is related to the possibility of evaluating the model within the time limit of the decision context - i.e., obtaining a predictive simulation result for a specific scenario in a shorter time than it takes to observe the scenario unfold in real-time. This latter is extremely important in high-risk scenarios, where our main aim is to prevent a critical scenario unfolding.
As there are an infinite number of potential critical scenarios for any high-risk system, and we are naturally restricted by finite computational limit, we need to prioritize our computational efforts sensibly way and be able to adapt to new information as it becomes available. These are the steps DNV recommends to enable an adaptive and virtual approach to system testing to ADVISE system owners on how to obtain reliable and necessary data for safe operation. We call this approach "ADVISE".
The first step towards understanding the response of a system is to probe the system, e.g., through virtual (or real) experiments. The second step is to be able to estimate the system response that occurs away from where the system has been probed. This is usually done by constructing a fast running approximation to the real response, often referred to as a surrogate model. The third step is to decide which experiments to run consequtively in order to maximize the information gained (including a risk-based objective). Finally we discuss how to improve surrogate models by imposing first principle constraints.
Below, we start by explaining what a surrogate model is (and some desired attributes), as this information is implicitly used in the other steps.
Surrogate models
Let us consider a complex computer model



If the evaluation of




Most ML algorithms create such surrogate models - fast approximations - based on a large set of training data. However, in addition to providing a fast approximation of a real process, A. O'Hagan, 2006 argues that to be able to perform reasonably good and efficient uncertainty analysis (UA) and sensitivity analysis (SA) of complex computer models, the surrogate model should also exhibit two other important traits. First, it should be possible to interpolate, i.e., ensure that all approximations match the observations exactly at the training points, and secondly it should be able to provide an uncertainty estimate of the prediction on all points that are not part of the training set (this is not typically available for many ML algorithms). Such a surrogate model is referred to as an emulator.
- Surrogate model
-
A surrogate model is an approximation
, established from a finite set of evaluations
.
- Emulator
-
An emulator is a surrogate model that can:
-
Interpolate. I.e.
for all training data
.
-
Provide uncertainty estimates on
for all data not in the training set
.
-
Interpolate. I.e.
For safety-critical systems, it is evident that not only being able to predict the outcome of a certain scenario, but also being able to acquire information on the confidence and uncertainty in that prediction is essential for safe operations and high-quality decision support.
Uncertainty Quantification (UQ) associated with use of complex (computer) models has been an active area of research in the Statistics community since the 1980s, and has had more recent interest from the Applied Mathematics community. Kennedy and O'Hagan, 2001 is one of the fundamental papers on UQ in complex mathematical (computer) models that addresses all sources of uncertainty encountered when using models to predict real world scenarios.
Uncertainty quantification related to such a function can be described by four types of UQ problems:
- Forward UQ
-
Uncertainty analysis. For a stochastic
, study the distribution of
.
-
Sensitivity analysis. Study how
responds to changes in
.
- Inverse UQ
-
Calibration. Estimate some
from noisy observations of the real process
.
-
Bias correction. Quantify model discrepancy.
Understanding the uncertainty of our approximations is how we establish confidence in our systems.
In the following sections, we outline how such emulators can be utilized with respect to real-time decision support and design of experiments to ensure safe designs. We also discuss how we can impose physics-based constraints on data driven models, and why this is worth doing.
Note that expensive or dangerous physical tests can be simulated using virtual models, and both real-world data and simulated data can be used to establish fast-running emulators, including uncertainty estimates. If we are able to replace the expensive and/or dangerous physical tests with simulations and construct fast-running emulators, we can guide our exploration of scenarios virtually that are not feasible to explore in the real world, and simultaneously obtain information on uncertainty related to the approximation.
EXAMPLE: Gaussian process emulator
Gaussian process (GP) is a stochastic process such that every finite collection of its random variables has a multivariate normal distribution. The distribution of a GP is the joint distribution of all those variables, and can be thought of as a distribution over functions. In an ML setting, the prediction of a GP regression algorithm will not only estimate the value at the point, but also include information on the uncertainty (i.e., the prediction is the marginal distribution of the GP at that point). See C.E. Rasmussen and C.K.I. Williams, 2006 for a comprehensive text on the use of GP in ML.
This example illustrates how GP regression - a type of supervised ML utilizing Bayesian inference - predicts a continuous quantity (as opposed to classification, which predicts discrete class labels).
Figure 8 shows a true function,

Figure 8: Example of Gaussian Process emulator with prediction and uncertainty bounds.
A different sample (and sample size) can be tested by changing the sample points input and clicking the re-sample button.
For typical experimental modeling situations, we do not have access to the function values themselves, only noisy data. Toggle the noise drop down to see the effect of noisy samples.
This example shows the core process of a GP regression model in one dimension. However, it is also applicable for high-dimensional input spaces.
Note, however, that higher dimensions require more observations for a GP model to give a meaningful prediction.
Design of experiments
Design-of-experiments (DOE) is a field of study that has its roots back in 1747 when James Lind carried out a systematic clinical trial to compare remedies for scurvy in British sailors. From this early beginning, the field has developed significantly, and, in 1935, the English statistician Ronald A. Fisher published one of the seminal books on the topic, The Design of Experiments.
Despite the science of design-of-experiments being a well-established field of study, modellers have a tendency to prefer non-optimal designs. A. Saltelli and P. Annoni, 2010 explain the tendency of modellers to prefer one-at-a-time (OAT) experimental designs, highlighting the aspects of:
- The baseline being a "safe" starting point where the model properties are well known (i.e., the best estimate).
- Changing one factor at the time ensures that whatever effect is observed on the output can be attributed to this factor alone.
- A non-zero effect implies influence, i.e., OAT do not make Type I errors (false positives).
These aspects make OAT approaches intuitive. However, to be a valid approach for UQ and SA, it must be assumed that all the probability density functions for the uncertain factors have sharp peaks on this multidimensional best-estimate point. This is not usually the case.
A. Saltelli and P. Annoni, 2010 also show how the curse-of-dimensionality proves that an OAT approach is inefficient with respect to exploring only a tiny fraction of a multidimensional input space. An OAT approach also has a tendency to miss important features of a response (see Example: Design-of-experiments below).
Example: Design-of-experiments
To illustrate some of the pitfalls in design of experiments and how we can improve this through an adaptive approach, we look at a simple, but non-linear, response function:

This function is the expensive function that we want to explore and learn. However, we will not only pretend that it is expensive to evaluate, we will also pretend that response values above a certain threshold become increasingly dangerous to evaluate. This will illustrate how we can include a risk perspective in our exploration.
Figure 9: A typical one-at-a-time sampling of the response function.
Figure 9 shows a typical sampling (15 points), where one factor has been changed at a time and the response of each sample has been obtained through experimental testing or simulations. If the figure is rotated, it is easy to see that the designer has selected an unfortunate combination of sampling points as they have almost the same response, z, in the x-direction for each y-value. If we fit a surrogate model to this data, then, based on these points, it will probably predict a smooth surface. Select the GP emulator tab to see a Gaussian process emulator fitted to these samples.
Figure 10: Gaussian process emulator of an OAT sampling.
The GP emulator fits the sample data perfectly (forced interpolation). However, as Figure 10 shows, the fit is not a good representation of the true function. This is one of the major pitfalls when convenient engineering practice is used to explore an unknown response. A better approach is to introduce a stochastic element to the sampling. The Latin Hypercube Sampling (LHS) is illustrated in the Latin Hypercube tab.
Note that the colours represent the estimated uncertainty in the emulator prediction, which is relatively high between the rows of x-valued samples and even higher in the extrapolation on either side.
Figure 11: Gaussian process emulator of a LHS sampling.
Using an LHS method, as illustrated in Figure 11, is clearly more efficient for exploring and learning the response of this function. A stochastic exploration of the input space is generally better at exposing non-linearities in a multidimensional response surface. Notice that an increase in the uncertainty estimate of the GP emulator corresponds well with an increasing difference between the true function and the prediction.
However, for a stochastic exploration like the LHS method, the analyst is stuck with the design, irrespective of what she learns from the first few samples. A more efficient way of utilizing information would be to make a small initial sample, and then base consecutive explorations on what has already been learned. Examples of such adaptive learning (AL) are illustrated in the next two tabs and Figure 14 below.
Figure 12: Gaussian process emulator of a LHS sampling with adaptive learning (AL) and local uncertainty reduction objective based on D.J.C. MacKay, 1992.
The black points in Figure 12 show the evaluated response of a 5 point initial LHS design. As the emulator gives an estimate of the prediction uncertainty, one AL approach is to implement an objective function that seeks to reduce the highest local uncertainty. This AL approach selects the input point with the highest estimate of prediction uncertainty and evaluates the true function at this point according to D.J.C. MacKay, 1992. A new emulator is then fitted to the new set of evaluation points, including the 5 initial points, and the latest evaluated point (light blue colour). The change in the GP emulator as new points are evaluated can be seen by changing the value of the slider below the plot.
As can be seen from the final emulator, based on 15 evaluation points, the AL approach by MacKay favours points on the outskirts of the input space (i.e., where the emulator extrapolates). This corresponds to exploring the limits of the operational space - and would most probably have detected the poor combination of relatively low speeds and sharp turn radius for the Mercedes Benz A-class design engineers. Another approach, with the objective to reduce the global uncertainty in the prediction across the input space, has been suggested by D.A. Cohn, 1996, and is illustrated in the AL global uncertainty tab.
Figure 13: Gaussian process emulator of an LHS sampling with adaptive learning (AL) and global uncertainty reduction objective based on D.A. Cohn, 1996.
Similarly to the local uncertainty reduction in the previous tab, it is possible to select points that reduce the global uncertainty, as suggested by D.A. Cohn, 1996. Figure 13 shows how the emulator prediction changes as new points are evaluated, based on the objective of reducing the global uncertainty in the response space. For this function and initial sampling points, this method selects points both in the interior of the input space as well as on the edges.
As illustrated in the examples above, there are several different methods to explore an unknown response space. The last two methods focus on reducing the uncertainty in the emulator prediction. Other algorithms have been developed e.g., for efficient optimization of global minima or maxima or contour estimation (see, e.g., J. Sacks et al., 1989, D.R. Jones et al., 1998, and P. Ranjan et al., 2008). These are just a few examples of the multitude of methods that exist.
For high-risk systems, it is prudent to include the consequence and risk perspective as well. The following sections describe and exemplify how we think that experiments (either physical or virtual) should be planned and designed. We need to combine different approaches and utilize the best of data-driven models and our phenomenological knowledge of both the physical processes and the associated consequences and risks.
Understand the critical scenarios
From a safety perspective, prudent exploration of the operational space should focus on the limit between inconsequential and critical scenarios. We want to be able to have an effective way to find contour(s) in the operational space that distinguish safe scenarios from unsafe scenarios. This means that we want to focus our testing efforts close to these contours. Expending test effort inside a region that is clearly a failure set is wasteful and potentially dangerous. Expending test efforts in a region that is clearly inconsequential is, from a safety perspective, also wasteful.
Thus, in order to be able to incorporate a risk perspective when exploring, we need to have a measure for both the consequence at different operational states, as well as a measure for the uncertainty associated with each operational state. This is where the added attributes of an emulator make it superior to ordinary ML surrogate models.
An example of an AL algorithm with a risk-based objective is illustrated below, where a risk measure has been included by comparing the estimated response against a capacity distribution.
EXAMPLE: Risk-based adaptive learning
Figure 14: Gaussian process emulator of an LHS sampling with adaptive learning (AL) and a risk-based objective.
Figure 14 shows an adaptive-learning process, where the objective is to identify a certain probability of failure (pof) level. We have performed a structural reliability analysis (SRA) to obtain pof estimates. This is based on the emulator prediction, with associated uncertainty, and a capacity distribution (shown in red on the back wall of the xz-plane. Modifying the contour estimation method from P. Ranjan, D. Bingham and G. Michailidis, 2008, the objective of AL here is to explore the region of the response space that corresponds to a target probability of failure (pof) set to 1%. The colour in the plot corresponds to the logarithmic pof level; blue signifies a pof below 0.1%, orange indicates a pof of 1%, and red shows a pof larger than 10%.
Having established such a pof contour, the analyst can continue with optimizing the operational conditions so that the system can be operated at a point where it maximizes its objective against the risk associated with the system failing.
Guide the AI - impose constraints
In order to increase confidence in the safe use of ML and AI in general engineering applications, Agrell et al., 2018 advocate adopting or developing models with certain attributes:
- Flexibility: The model should be flexible enough to represent a broad class of functions.
- Constrainability: It should be possible to impose constraints on the model based on phenomenological knowledge.
- Probabilistic inference: The model output should be represented by a distribution at any point of the model range.
For engineering purposes, an ML model should be flexible enough to capture the often complex behaviour of a physical process - without prior knowledge of the function form (i.e., linear, polynomial, exponential, sinusodial, etc.). This flexibility is achieved by most non-parametric ML models, as well as popular parametric models, through various techniques (see, e.g., T. Hastie et al., 2009 for details) .
The possibility of imposing constraints on a model can help to make an opaque model more transparent. By a transparent model, we mean a model that has a relationship between inputs and output that can be understood by humans, and the characteristic properties and limitations of the model can be understood without explicit computation (e.g., a linear regression with linear basis). In contrast, advanced ML methods are often considered opaque, i.e., black-box models. These models are so complex that a human cannot understand the relationship between the model's inputs and its output.
The scientific method is based on the principle that any model, or hypothesis, should be falsifiable. All models, including ML models, are based on a set of assumptions. To be able to falsify a model or its assumptions, it must, in principle, be possible to make an observation that would show the assumption to be false. Transparency is one way of falsifying a model; however, many ML models are opaque, and falsification is usually based on measures of poor prediction accuracy (e.g., tests to check for overfitting - see T. Hastie et al., 2009 for details).
For complex and high-risk engineering systems, it might be difficult to obtain the observations that are needed to assess the validity of the model in regions with serious consequences from erroneous predictions.
However, if constraints based on phenomenological knowledge can be imposed, the problem of overfitting has the potential to be significantly reduced. Known physical constraints would increase confidence in extrapolation outside the data on which the model was trained, and this would increase the robustness of the model and its performance for application on future data. Figure 15 illustrates three relevant constraints that are often applicable to physical systems based on differential inequalities.

Figure 15: Example functions fitted to three observations for no constraints, an upper bounded function, a monotonic function, and a convex function.
The three constraints in Figure 15 can be described mathematically by:



A large variation in unconstrained functions can potentially be fitted to these observations and, if the model is opaque, the only way to characterize and assess the model fully is through exhaustive evaluation for all possible inputs. By imposing an upper bound, the analyst ensures that the prediction will never exceed a certain value, and the response space is reduced.
Where the bound constraint limits the response space, the monotone and convex constraints will limit the form of possible functions, and can, depending on the observed points, be very strong constraints. The models can be further restricted by imposing combinations of multiple constraints. This can be thought of as putting a black-box model inside a white box, enabling deduction of bounds on the model properties through the imposed constraints. This is an area of recent research (see, e.g., H. Maatouk, X. Bay, 2017 and T. Yu, 2007).
Where outputs from ML models are to be used for risk and reliability applications, probabilistic inference is essential. Model predictions in the form of fixed values and best estimates are not applicable. The danger of expressing risk through expected values is that it may hide valuable information about potentially catastrophic scenarios. Modern definitions of risk are therefore usually related to a distribution over potential outcomes. A common metric for quantifying the uncertainty of an ML model is the probability used to describe model accuracy (e.g., the fraction of correctly classified dogs in a set of animal images). However, the fact that a model has an acceptable accuracy 99% of the time might be meaningless if an erroneous prediction in the remaining 1% is associated with severe consequences. The traditional approach to compensating for this has been to scrutinize the model by human quality control measures to ensure an acceptable maximum prediction error - usually on the conservative side. This might no longer be feasible for higher dimensional models, which, more often than not, are opaque. One way to mitigate this is to use models that can estimate the uncertainty of their predictions on their own. This is why Bayesian methods have an advantage over other ML methods, when ML is used either to evaluate risk or to make predictions for high-risk systems. A relevant podcast on AI decision making and Bayesian methods can be found on Data Skeptic - AI Decision Making.
DNV argues that artificial intelligence - or data analytics - can be guided to a much more accurate answer if we introduce causal knowledge about the problem at hand, and include known constraints about the underlying physical, or causal, processes. We urge the industry to be active in following and contributing to research in these areas to enable safer use of ML and AI in engineering problems where risk is a factor.
References
"The Dark Secret at the Heart of AI" MIT Technology review, vol. 120 No. 3 2017. [web]
"Three Principles of Data Science: Predictability, Stability and Computability" KDD'17 Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Denver, USA, 1988.
A. Blum and R.L. Rivest (1988)
"Training a 3-node neural network is NP-complete" NIPS 1988, Proceedings of Advances in Neural Information Processing Systems 1, Halifax, Canada, Aug. 13.-17., 2017. _[pdf]
D. Sculley, J. Snoek, A. Rahimi, A. Wiltschko (2018)
"Winner's curse? On pace, progress, and empirical rigor" Sixth International Conference on Learning Representations, Vancouver, Canada, Apr. 30. - May 3., 2018. [pdf]
"Some studies in machine learning using the game of Checkers." IBM Jourtnal of research and development, 1959. [pdf]
"A few useful things to know about machine learning" Communications of the ACM, Vol. 55 No. 10, Pages 78-87, 2012. [pdf]
T. Hastie, R. Tibshirani, and J. Friedman (2009)
"The Elements of Statistical Learning: Data Mining, Inference, and Prediction." 2nd Edition, Springer, Springer series in statistics, 2009. [pdf]
"The Future Computed: Artificial Intelligence and its role in society" Microsoft Corporation, ISBN 977-0-999-7508-1-0, 2018. [pdf]
"Concrete Problems in AI Safety" arXiv:1606.06565, 2016. [pdf]
"Executive Summary - The Future Computed: Artificial Intelligence and its role in society" Microsoft Corporation, ISBN 977-0-999-7508-1-0, 2018. [pdf]
EU General Data Protection Regulation (2016)
"General Data Protection Regulation" Council of the European Union, Brussels, 2016. [pdf]
"After the Facebook scandal: The grand plan to hold AI to account" New Scientist, 11. April 2018.
"Weapons of math destruction: How big data increases inequality and threatens democracy." Broadway Books, 2017.
A. Brandsæter and K.E. Knutsen (2018) - (in press)
"Towards a framework for assurance of autonomous navigation systems in the maritime industry", European Safety and Reliability Conference, ESREL 2018, Trondheim, Norway, 2018. [pdf]
"The mathematics of causal relations." In P.E. Shrout, K. Keyes, and K. Ornstein (Eds.), Causality and Psychopathology: Finding the Determinants of Disorders and their Cures, Oxford University Press, 47-65, 2010. [pdf]
"Causality: Models, Reasoning, and Inference" Cambridge University Press, New York. 2nd Edition 2009.
"Theoretical Impediments to Machine Learning With Seven Sparks from the Causal Revolution" arXiv preprint, arXiv:1801.04016, 2018. [pdf]
Y. Hagmayer, S.A. Sloman, D.A. Lagnado, & M.R. Waldmann (2007)
"Causal reasoning through intervention." Causal learning: Psychology, philosophy, and computation: 86-100, 2007. [pdf]
"The Problem with the Data-Information-Knowledge-Wisdom Hierarchy" Harvard Business Review, February 2., 2010.
C. Agrell, S. Eldevik, A. Hafer, F.B. Pedersen, E. Stensrud (2018) - (in press)
"Pitfalls of machine learning for tail events in high risk environments", European Safety and Reliability Conference, ESREL 2018, Trondheim, Norway, 2018.
"Autonomous Precision Landing of Space Rockets", Winter Bridge on Frontiers of Engineering, Vol. 4, Issue 46, pp.15-20, December 19., 2016. [pdf]
M.P. Allen and D.J. Tildesley (1991)
"Computer simulation of Liquids", 2nd Ed., Clarendon press, Oxford, 1991. [pdf]
"Robustness in the strategy of scientific model building" in R.L. Launer, G.N. Wilkinson, Robustness in Statistics, Academic Press, pp. 201–236, 1979. [pdf]
O. Ditlevsen, H.O. Madsen (1996)
"Structural reliability methods." John Wiley & Sons Ltd, 1996. [pdf]
"Mercedes-Benz tries to put a persistent moose problem to rest." NY Times, December 11. 1997.
"Mercedes bends" The Economist, November 13. 1997.
M.C. Kennedy and A. O'Hagan (2001)
"Bayesian calibration of computer models" Journal of the Royal Statistical Society, B 63, Part 3, pp.425-464, 2001. [pdf]
"Bayesian analysis of computer code outputs: A tutorial" Reliability Engineering & System Safety, Vol. 91, Issue 10-11, pp1290-1300, 2006. [pdf]
C.E. Rasmussen and C.K.I. Williams (2006)
"Gaussian processes for machine learning." The MIT Press, 2006. [pdf]
"The Design of Experiments", 2nd Ed., Oliver and Boyd, Edinburgh, 1937. [pdf]
A. Saltelli and P. Annoni (2010)
"How to avoid a perfunctory sensitivity analysis" Environmental Modelling & Software, Vol. 25, Issue 12, pp. 1508-1517 2010. [pdf]
"Information-based objective functions for active data selection." Neural Computation, 1992, 4.4: 590-604. [pdf]
"Neural network exploration using optimal experiment design." Neural Networks, 1996, 9.6: 1071-1083. [pdf]
J. Sacks, W.J. Welch, T.J. Mitchell and H.P. Wyn (1989)
"Design and Analysis of Computer Experiments." Statistical Science, ol. 4, no. 4, 1989, pp. 409–423. [pdf]
D.R. Jones, M. Schonlau and W.J. Welch (1998)
"Efficient global optimization of expensive black-box functions." Journal of Global Optimization, 1998, 13.4: 455-492. [pdf]
P. Ranjan, D. Bingham and G. Michailidis (2008)
"Sequential experiment design for contour estimation from complex computer codes." Technometrics, 2008, 50.4: 527-541. [pdf]
"Incorporating prior domain knowledge into inductive machine learning: its implementation in contemporary capital markets" PhD Thesis, University of Tech., Sydney, Faculty of Information Technology 2007. [pdf]
"Gaussian process emulators for computer experiments with inequality constraints", Mathematical Geosciences Vol. 49, 5, pp. 557-582, 2017. [pdf]
Plotting and web-app library
"Dash by plotly", v. 0.19.0



